According to the Bohr model of the atom, electrons exist in quantized energy levels surrounding the atom's nucleus. These energy levels are described by the principal quantum number n = 1, 2, 3, ... . Electrons may only exist in these states, and may only transit between these states.
The set of transitions from n ≥ 3 to n = 2 is called the Balmer series and its members are named sequentially by Greek letters:
* n = 3 to n = 2 is called Balmer-alpha or H-alpha,
* n = 4 to n = 2 is called H-beta,
* n = 5 to n = 2 is called H-gamma, etc.
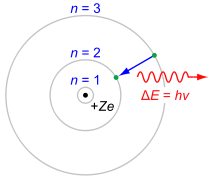
H-alpha Emission: In the simplified Rutherford Bohr model of the hydrogen atom, the Balmer lines result from an electron jump between the second energy level closest to the nucleus, and those levels more distant. The \scriptstyle 3 \rightarrow 2 transition depicted here produces an H-alpha photon, and the first line of the Balmer series. For hydrogen (Z = 1) this transition results in a photon of wavelength 656 nm (red).
For the Lyman series the naming convention is:
* n = 2 to n = 1 is called Lyman-alpha,
* n = 3 to n = 1 is called Lyman-beta, etc.
H-alpha has a wavelength of 6562.81 Å, is visible in the red part of the electromagnetic spectrum, and is the easiest way for astronomers to trace the ionized hydrogen content of gas clouds. Since it takes nearly as much energy to excite the hydrogen atom's electron from n = 1 to n = 3 as it does to ionize the hydrogen atom, the probability of the electron being excited to n = 3 without being removed from the atom is very small. Instead, after being ionized, the electron and proton recombine to form a new hydrogen atom. In the new atom, the electron may begin in any energy level, and subsequently cascades to the ground state (n = 1), emitting photons with each transition. Approximately half the time, this cascade will include the n = 3 to n = 2 transition and the atom will emit H-alpha light. Therefore, the H-alpha line occurs where hydrogen is being ionized.
The H-alpha line saturates (self-absorbs) relatively easily because hydrogen is the primary component of nebulae, so while it can indicate the shape and extent of the cloud, it cannot be used to accurately determine the cloud's mass. Instead, molecules such as carbon dioxide, carbon monoxide, formaldehyde, ammonia, or methyl cyanide are typically used to determine the mass of a cloud.

The four visible hydrogen emission spectrum lines in the Balmer series. The red line at far-right is H-alpha
A hydrogen-alpha filter is an optical filter designed to transmit a narrow bandwidth of light generally centered on the H-alpha wavelength. They are characterized by a bandpass width that measures the width of the wavelength band that is transmitted.[1] These filters are manufactured by multiple (~50) layers of vacuum-deposited layers. These layers are selected to produce interference effects that filter out any wavelengths except at the requisite band.[2]
Alternatively, an etalon(see: Fabry–Pérot interferometer) may be used as the narrow band filter (in conjunction with a "blocking filter" or energy rejection filter) to pass only a narrow (<1 Å) range of wavelengths of light centred around the H-Alpha emission line. The physics of the etalon and the dichroic interference filters are essentially the same (relying on constructive/destructive interference of light reflecting between surfaces), but the implementation is different (an interference filter relies on the interference of internal reflections). Due to the high velocities sometimes associated with features visible in h-alpha light (such as fast moving prominences and ejections), solar h-alpha etalons are often able to be tuned (by tilting or changing the temperature) to cope with the associated Doppler effect.
